IT'S ALL ABOUT LIFE, COLLAGE AND FRIENDSHIP: ALJABAR LINEAR

PERKENALAN

Nama : Muhamad Ikhsan Ramli

NIM : 1133368672

Jenis Kelamin : Laki - Laki

Alamat : Kp. Cengkok RT. 08/04 Kec. Balaraja Kab. Tangerang - Banten

Pekerjaan : Mahasiswa

Study : Teknik Informatika D3 - Artifical Informatisc di Perguruan Tinggi Raharja

ALASAN SAYA MASUK RAHARJA

Alasan saya masuk raharja yaitu karena menurut saya perguruan tinggi raharja sudah memiliki nilai akreditasi yang baik yaitu B untuk jurusan Teknik Informatika dan juga memiliki fasilitas yang bagus tentunya, seperti fasilitas kelas i-learning yang menggunakan ipad dalam metode pembelajaran, karena bisa lebih efektif dan juga saya senang dengan dosen yang mengajar di perguruan tinggi raharja yang rata-rata usianya masih muda sehingga saya sebagai mahasiswa betah dalam mengikuti semua mata kuliah yang ada di perguruan tinggi raharja, apalagi kalo ibu diah yang mengajar pasti semua mahasiswa akan mengerti dengan cepat walaupun mata kuliah yang di ajarkan tidak mudah yaitu ALJABAR LINEAR !!

dan juga tempat kuliah perguruan tinggi raharja tidak jauh dari rumah saya sehingga memudahkan dalam berbagai hal, dan tempat tongkrongan yang di bagi menjadi 2 yaitu : Kantin atas untuk yang tidak merokok dan Kantin bawah untuk para perokok, sehingga saya bisa terbebas dari asap rokok, karena saya mempunyai penyakit Sesak napas ( ASMA ) hehehehe !!

Masih banyak lagi alasan kenapa saya memilih kuliah di perguruan tinggi raharja tapi untuk mempersingkat waktu saya cukupkan saja !!

TUGAS MAKALAH

STATUS : TERPENUHI

KETERANGAN : DAPAT DILIHAT DI BAWAH

KELOMPOK 9

JUDUL MAKALAH : INAVERS MATRIK

ANGGOTA : - MUHAMAD IKHSAN RAMALI

- TEGAR GUNTARA

- YUSUP HADI

- NURKAH MAHENDRA

- RONAL RAIVARDO

Matriks Balikan (Invers)

JIka A dan B matriks bujur sangkar sedemikian rupa sehingga A B = B A = I , maka B disebut balikan atau invers dari A dan dapat dituliskan

B = A - 1

( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan

A = B - 1

. Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.
Matriks A = $\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}$ dapat di-invers apabila ad - bc ≠ 0
Dengan Rumus =
$A^{-1} = \frac{1} {ad-bc}\begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix} = \begin{bmatrix} \frac{d} {ad-bc} & -\frac{b} {ad-bc} \\ -\frac{c} {ad-bc} & \frac{a} {ad-bc} \\ \end{bmatrix}$
Apabila A dan B adalah matriks seordo dan memiliki balikan maka AB dapat di-invers dan

(A B) - 1 = B - 1 A - 1

Contoh 1:
Matriks

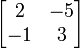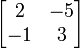
A = $\begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix}$ dan B = $\begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}$

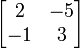AB = $\begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix}$ $\begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}$ = $\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}$ = I (matriks identitas)

BA = $\begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}$ $\begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix}$ = $\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}$ = I (matriks identitas)

Maka dapat dituliskan bahwa

B = A - 1

(B Merupakan invers dari A)

Contoh 2:
Matriks

A = $\begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix}$ dan B = $\begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}$

AB = $\begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix}$ $\begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}$ = $\begin{bmatrix} 3 & 4 \\ 6 & 8 \\ \end{bmatrix}$

BA = $\begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}$ $\begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix}$ = $\begin{bmatrix} 17 & 21 \\ 15 & 19 \\ \end{bmatrix}$

Karena AB ≠ BA ≠ I maka matriks A dan matriks B disebut matriks tunggal.

Contoh 3:
Matriks

A = $\begin{bmatrix} 3 & 1 \\ 5 & 2 \\ \end{bmatrix}$

Tentukan Nilai dari A^-1
Jawab:
$A^{-1} =\frac{1} {(3)(2)-(5)(1)}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \frac{1} {6-5}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \frac{1} {1}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix}$

Contoh 4:
Matriks

A = $\begin{bmatrix} 1 & 2 \\ 1 & 3 \\ \end{bmatrix}$ , B = $\begin{bmatrix} 3 & 2 \\ 2 & 2 \\ \end{bmatrix}$ , AB = $\begin{bmatrix} 7 & 6 \\ 9 & 8 \\ \end{bmatrix}$

Dengan menggunakan rumus, maka didapatkan

$A^{-1} = \begin{bmatrix} 3 & -2 \\ -1 & 1 \\ \end{bmatrix}$ , $B^{-1} = \begin{bmatrix} 1 & -1 \\ -1 & \frac{3} {2} \\ \end{bmatrix}$ , $(AB)^{-1} = \begin{bmatrix} 4 & -3 \\ -\frac{9} {2} & 8 \\ \end{bmatrix}$

Maka

$B^{-1} A^{-1}= \begin{bmatrix} 1 & -1 \\ -1 & \frac{3} {2} \\ \end{bmatrix}$ $\begin{bmatrix} 3 & -2 \\ -1 & 1 \\ \end{bmatrix}$ = $\begin{bmatrix} 4 & -3 \\ -\frac{9} {2} & 8 \\ \end{bmatrix}$